Geodesic buffers
Buffers polygons delimite areas that are within some distance of input features. We can have them arround points or lines. We will show here examples of both.
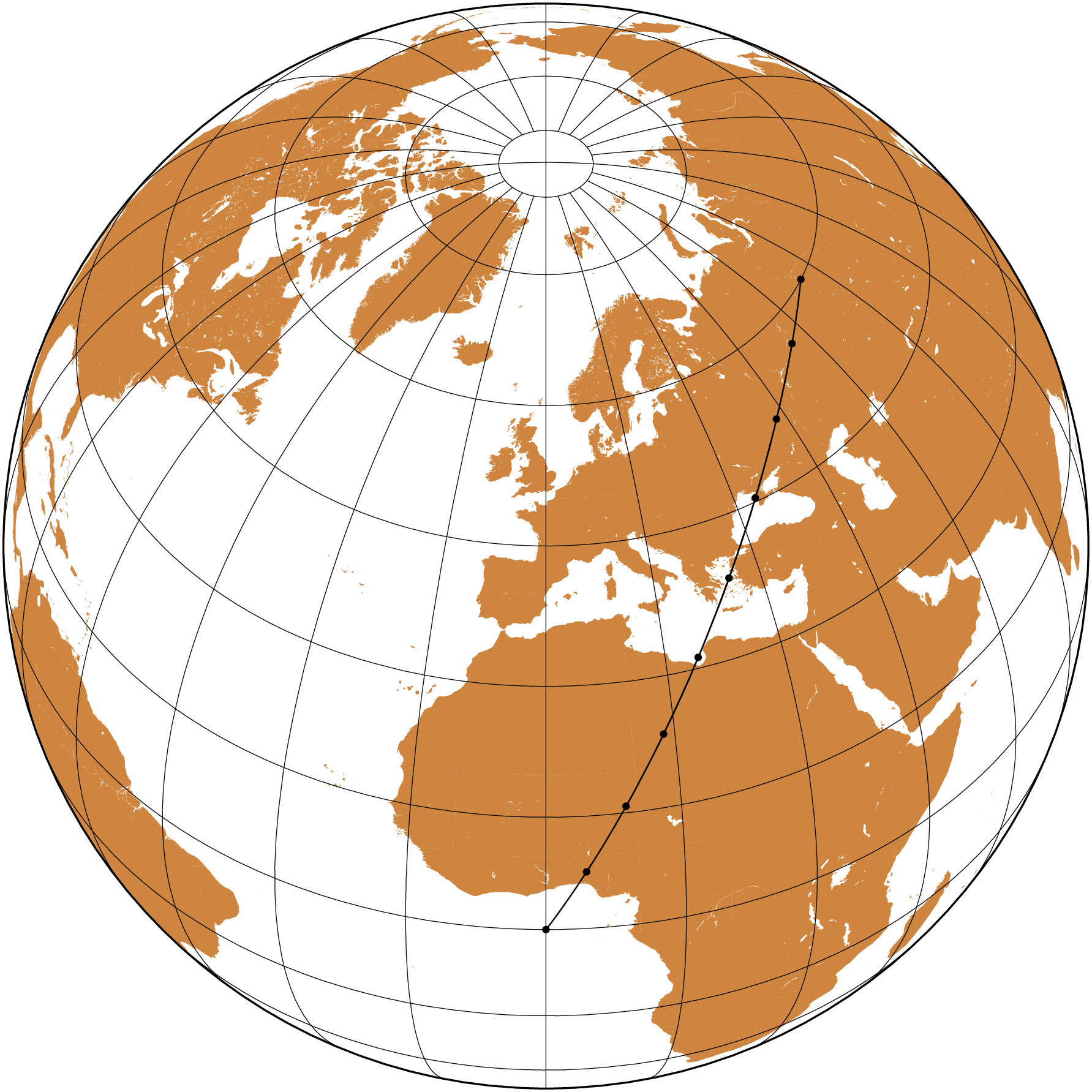
We start by computing a great circle, also known as an orthodrome between two points and interpolated at 1000 km increments.
using GMT
# Compute the great circle (orthodrome) line
ortho = orthodrome([0 0; 70 60], step=1000, unit=:k);
# Plot the orthodrome on an orthographic projection
coast(region=:global, proj=(name=:ortho, center=(0,45)), land=:peru, frame=:g)
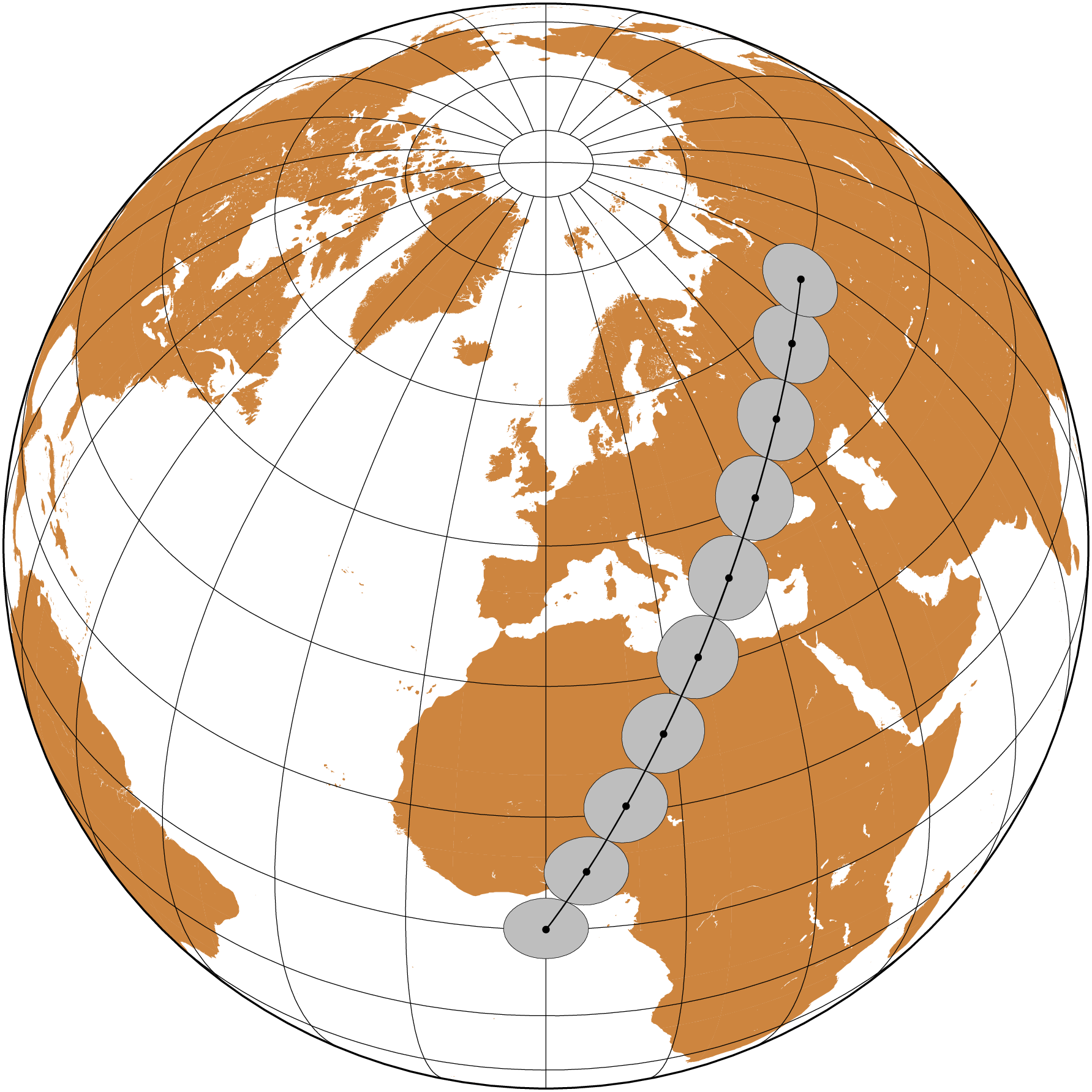
plot!(ortho, lw=0.5, marker=:circ, ms=0.1, fill=:black, show=true)Next we will draw geodesic circles with 500 km radius with center on the orthodrome vertices. And to do it we need ofc to compute those circles. We compute the circles with the circgeo function.
using GMT
ortho = orthodrome([0 0; 70 60], step=1000, unit=:k);
c = circgeo(ortho, radius=500, unit=:k);
coast(region=:global, proj=(name=:ortho, center=(0,45)), land=:peru, frame=:g)
plot!(c, lw=0.1, fill=:gray)
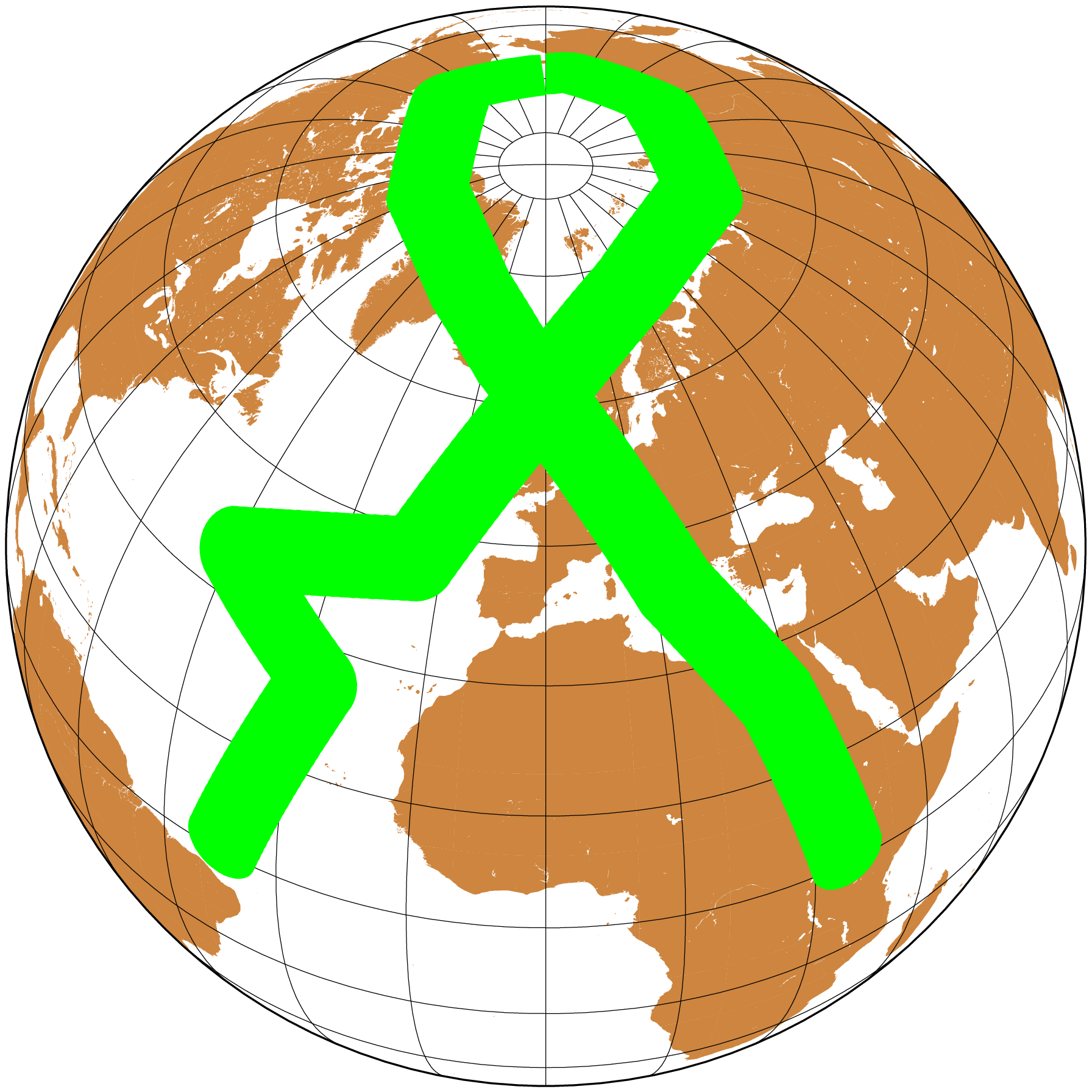
plot!(ortho, lw=0.5, marker=:circ, ms=0.1, fill=:black, show=true)Now imagine that we plot many close circles and compute the union of them all. That's how we get the buffer.
using GMT
# Poly-line arround which to compute the buffer. Make it go arround the pole.
line = [-37. 1; -28 26; -45 35; -19 42; -9 55; 4 64; 32 72; 85 73; 135 73; 172 73; -144 73; -78 77; -27 72; -8 65; 8 54; 18 39; 28 24; 34 1];
D = buffergeo(line, width=500000); # Compute the buffer polygon
coast(region=:global, land=:peru, frame=:g,
proj=(name=:ortho, center=(0,45)),
plot=(data=D, fill=:green), show=true)
© GMT.jl. Last modified: May 19, 2025. Website built with Franklin.jl and the Julia programming language.
These docs were autogenerated using GMT: v1.29.0