(3) Spectral estimation and xy-plots
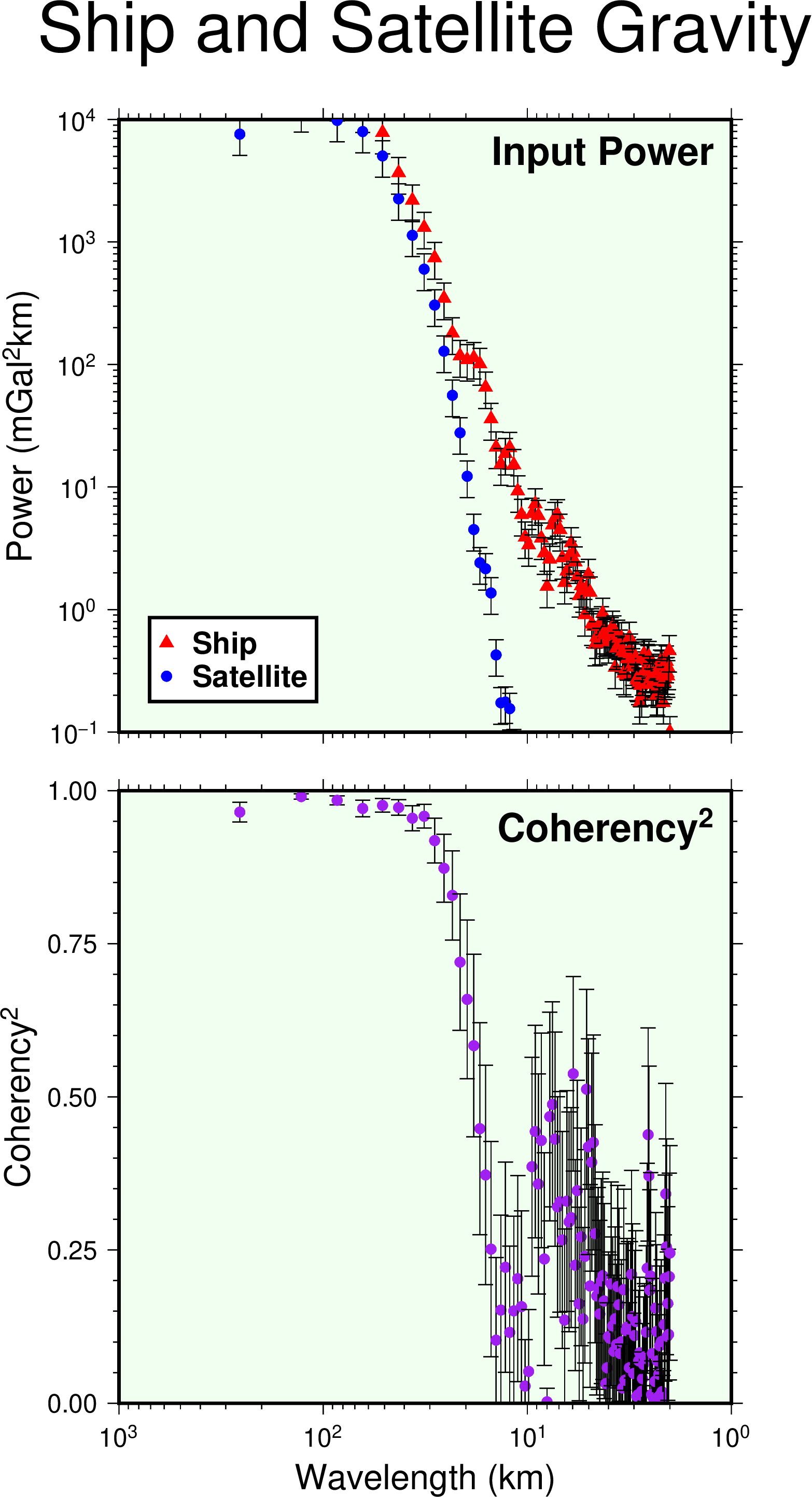
In this example we will show how to use the GMT programs fitcircle, project, sample1d, spectrum1d, and plot. Suppose you have (lon, lat, gravity) along a satellite track in a file called sat.xyg, and (lon, lat, gravity) along a ship track in a file called ship.xyg. You want to make a cross-spectral analysis of these data. First, you will have to get the two data sets into equidistantly sampled time-series form. To do this, it will be convenient to project these along the great circle that best fits the sat track. We must use fitcircle to find this great circle and choose the L2 estimates of best pole. We project the data using project to find out what their ranges are in the projected coordinate. The script computes the common range. We can then resample the projected data, and carry out the cross-spectral calculations, assuming that the ship is the input and the satellite is the output data. The final plot example_03.ps shows the ship and sat power in one diagram and the coherency on another diagram, both on the same page, with an auto-generated legend. Thus, the complete automated script reads:
The final illustration shows that the ship gravity anomalies have more power than altimetry derived gravity for short wavelengths and that the coherency between the two signals improves dramatically for wavelengths > 20 km.
using GMT
# First, we use "fitcircle" to find the parameters of a great circle
# most closely fitting the x,y points in "sat_03.txt":
cpos = fitcircle("@sat_03.txt", norm=2, coordinates=:mean, par=(IO_COL_SEPARATOR="/",))
ppos = fitcircle("@sat_03.txt", norm=2, coordinates=:north, par=(IO_COL_SEPARATOR="/",))
# Now we use "project" to project the data in both sat_03.txt and ship_03.txt
# into data.pg, where g is the same and p is the oblique longitude around
# the great circle. We use "km" to get the p distance in kilometers, and "sort"
# to sort the output into increasing p values.
sat_pg = project("@sat_03.txt", origin=cpos, pole=ppos, sort=true, outvars=:pz, km=true)
ship_pg = project("@ship_03.txt", origin=cpos, pole=ppos, sort=true, outvars=:pz, km=true)
# Get the common extrema values rounded to 1 km
bounds = round.([max(sat_pg.bbox[1], ship_pg.bbox[1]) min(sat_pg.bbox[2], ship_pg.bbox[2])], digits=0)
samp_x = collect(bounds[1]:bounds[2])
# Now we can resample the gmt projected satellite data:
samp_sat_pg = sample1d(sat_pg, range=samp_x)
# For reasons above, we use filter1d to pre-treat the ship data. We also need to sample
# it because of the gaps > 1 km we found. So we use filter1d | sample1d. We also
# use the "ends" on filter1d to use the data all the way out to bounds :
D = filter1d(ship_pg, filter=:m1, range=(bounds[1], bounds[2], 1), ends=true)
samp_ship_pg = sample1d(D, range=samp_x)
# Now to do the cross-spectra, assuming that the ship is the input and the sat is the output
# data, we do this:
D = spectrum1d([samp_ship_pg[:,2] samp_sat_pg[:,2]], size=256, sample_dist=1,
wavelength=true, outputs=(:xpower, :ypower, :coherence))
# Time to plot spectra
subplot(grid=(2,1), margins="0.3c", col_axes=(bott=true, label="Wavelength (km)"),
autolabel=(anchor=:TR, offset="8p"), title="Ship and Satellite Gravity",
panel_size=10, frame=(axes="WeSn", bg="240/255/240"))
gmtset(FONT_TAG="18p,Helvetica-Bold",)
subplot(:set, panel=(1,1), autolabel="Input Power")
plot(D[:Wavelength, :Xpower, :σ_Xpow], proj=:loglog, flip_axes=:x, xaxis=(annot=1, ticks=3, scale=:pow),
yaxis=(annot=1, ticks=3, scale=:pow, label="Power (mGal@+2@+km)"), fill="red", marker=:Triangle,
ms="5p", region=(1,1000,0.1,10000), error_bars=(y=true, pen=0.5), legend="Ship")
plot(D[:Wavelength, :Ypower, :σ_Ypow], fill="blue", marker=:circ, ms="5p",
error_bars=(y=true, pen=0.5), legend="Satellite")
legend(pos=(anchor="BL", offset=0.5), box="+gwhite+pthicker", par=(FONT_ANNOT_PRIMARY="14p,Helvetica-Bold",))
subplot(:set, panel=(2,1), autolabel="Coherency@+2@+")
plot(D[:Wavelength, :Coher, :σ_Coher], region=(1,1000,0,1), proj=:logx, flip_axes=:x,
xaxis=(annot=1, ticks=3, scale=:pow, label="Wavelength (km)"),
yaxis=(annot=0.25, ticks=0.05, label="Coherency@+2@+"), marker=:circ, ms="5p",
fill=:purple, error_bars=(y=true, pen=0.5))
subplot(:show)These docs were autogenerated using GMT: v1.16.0