whittaker

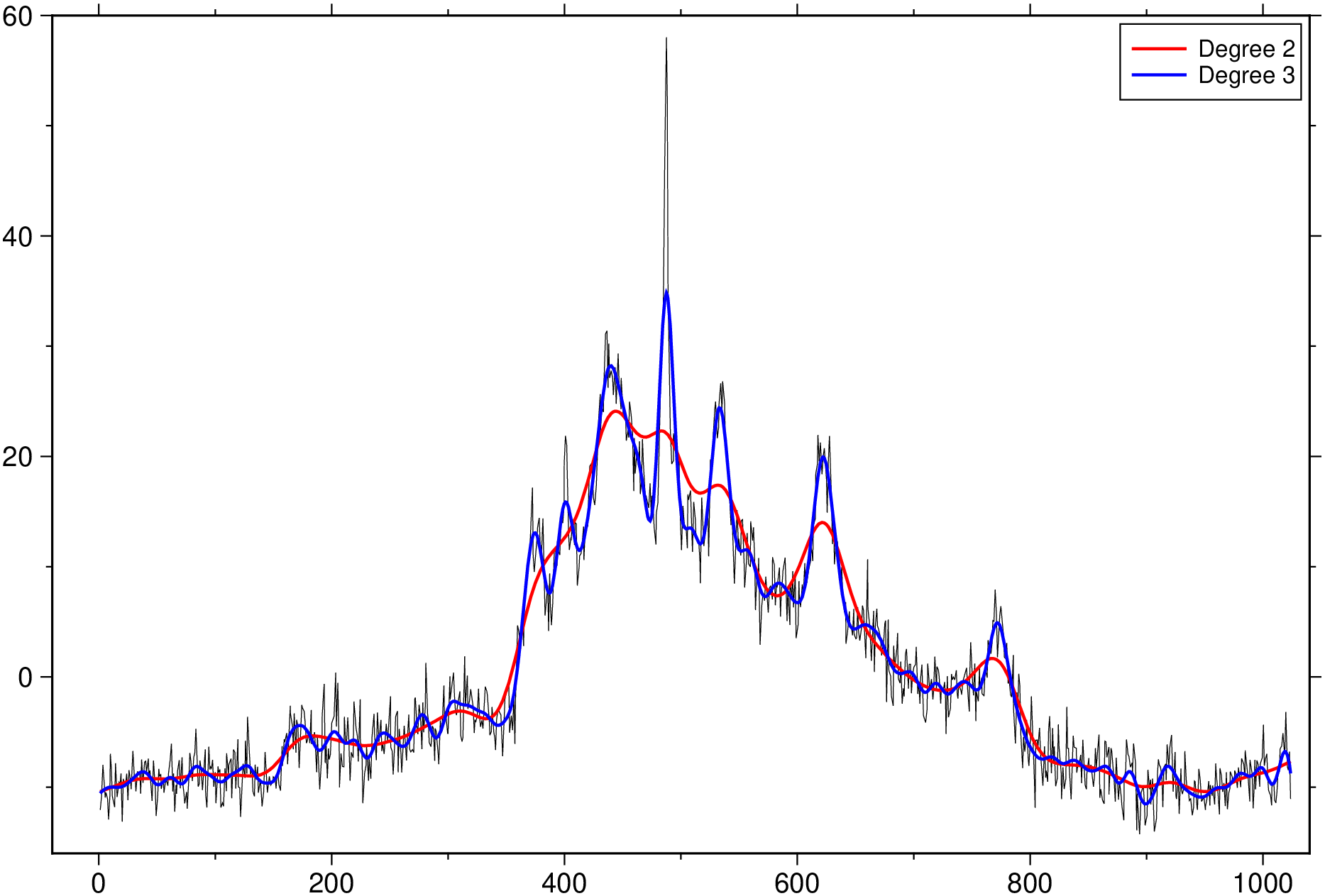
Dout = whittaker(D::GMTdataset, lambda, d=2; weights=nothing)

or

z = whittaker(x::AbstractVecOrMat{<:Real}, y::VecOrMat{<:Real}, lambda, d=2; weights=nothing)

Perform a Whittaker-Henderson smoothing and interpolation.

Args

  • D: A GMTdatset with a x,y data series.
  • x,y: In alternative to the D form, pass vectors of x and y.
  • lambda: Smoothing parameter; large lambda gives smoother result.
  • d: Order of differences (default = 2).

Kwargs

  • weights: Weights (0/1 for missing/non-missing data). Note, if input y contains NaNs, we replace them by a another flag value and automatically set w.

Citations

  • A Perfect Smoother (https://pubs.acs.org/doi/10.1021/ac034173t)
  • ‘Smoothing and interpolation with finite differences’. Eilers P. H. C, 1994. (http://dl.acm.org/citation.cfm?id=180916)
  • Transtaled to Julia from Matlab code from ‘A Perfect Smoother’. Paul H. C. Eilers. Analytical Chemistry 2003 75 (14), 3631-3636. DOI: 10.1021/ac034173t

Examples

using GMT

D = gmtread(TESTSDIR * "/assets/nmr_with_weights_and_x.csv");
D2 = whittaker(D, 2e4, 2);
D3 = whittaker(D, 2e4, 3);
plot(D)
plot!(D2, lc=:red, lt=1, legend="Degree 2")
plot!(D3, lc=:blue, lt=1, legend="Degree 3", show=true)

t = 2001:0.003:2007;
_v = 5*cospi.((t .- 2000)/2); v = _v + (5*rand(length(t)) .- 2.5);
v[2002.6 .< t .< 2003.4] .= NaN;
z = whittaker(t, v, 0.01, 3);
plot(t, v, legend="Noisy", plot=(data=[t _v], lc=:green, lt=1, legend="Original"))
plot!(t, z, lc=:red, lt=1, legend="Degree 3", show=true)

Source Code

This function has multiple methods:

See Also

lowess, hampel

Alphabetical Function List