lowess

lowess(x, y, span = 2 / 3, nsteps = 3, delta = 0.01 * (maximum(x) - minimum(x)))

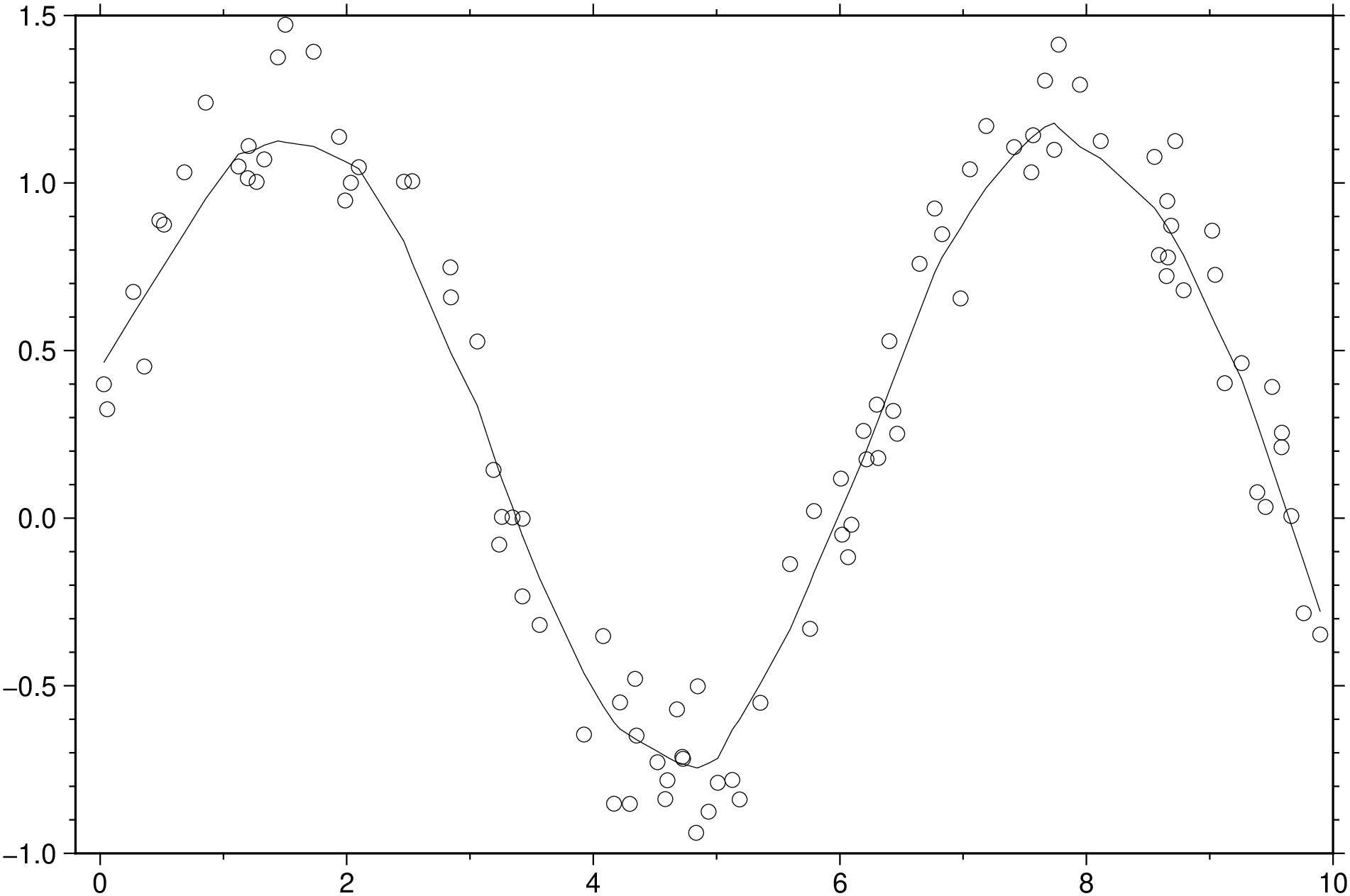
Compute the smooth of a scatterplot of y against x using robust locally weighted regression. Input vectors x and y must contain either integers or floats. Parameters span and delta must be of type T, where T <: AbstractFloat. Returns a vector ys; ys[i] is the fitted value at x[i]. To get the smooth plot, ys must be plotted against x.

Arguments

• x::Vector: Abscissas of the points on the scatterplot. x must be ordered.
• y::Vector: Ordinates of the points in the scatterplot.
• span: The amount of smoothing.
• nsteps::Integer: Number of iterations in the robust fit.
• delta: A nonnegative parameter which may be used to save computations. Default is 0.01 * (maximum(x) - minimum(x)).

Example

using GMT

x = sort(10 .* rand(100))
y = sin.(x) .+ 0.5 * rand(100)
ys = lowess(x, y, span=0.2)
scatter(x, y)
plot!(x, ys, show=true)

Source Code

This function has multiple methods:

• lowess(x::AbstractVector{T}, y::AbstractVector{T}; span, nsteps, delta) where T<:AbstractFloat - lowess.jl:49
• lowess(mat::Matrix{<:Real}; span, nsteps, delta) - lowess.jl:43
• lowess(x::AbstractVector{R}, y::AbstractVector{S}; span, nsteps, delta) where {R<:Real, S<:Real} - lowess.jl:38
• lowess(D::GMTdataset; span, nsteps, delta) - lowess.jl:31

See Also

whittaker, hampel

Alphabetical Function List